122-year-old Triangle-to-Square Puzzle Solution Confirmed as Best Possible
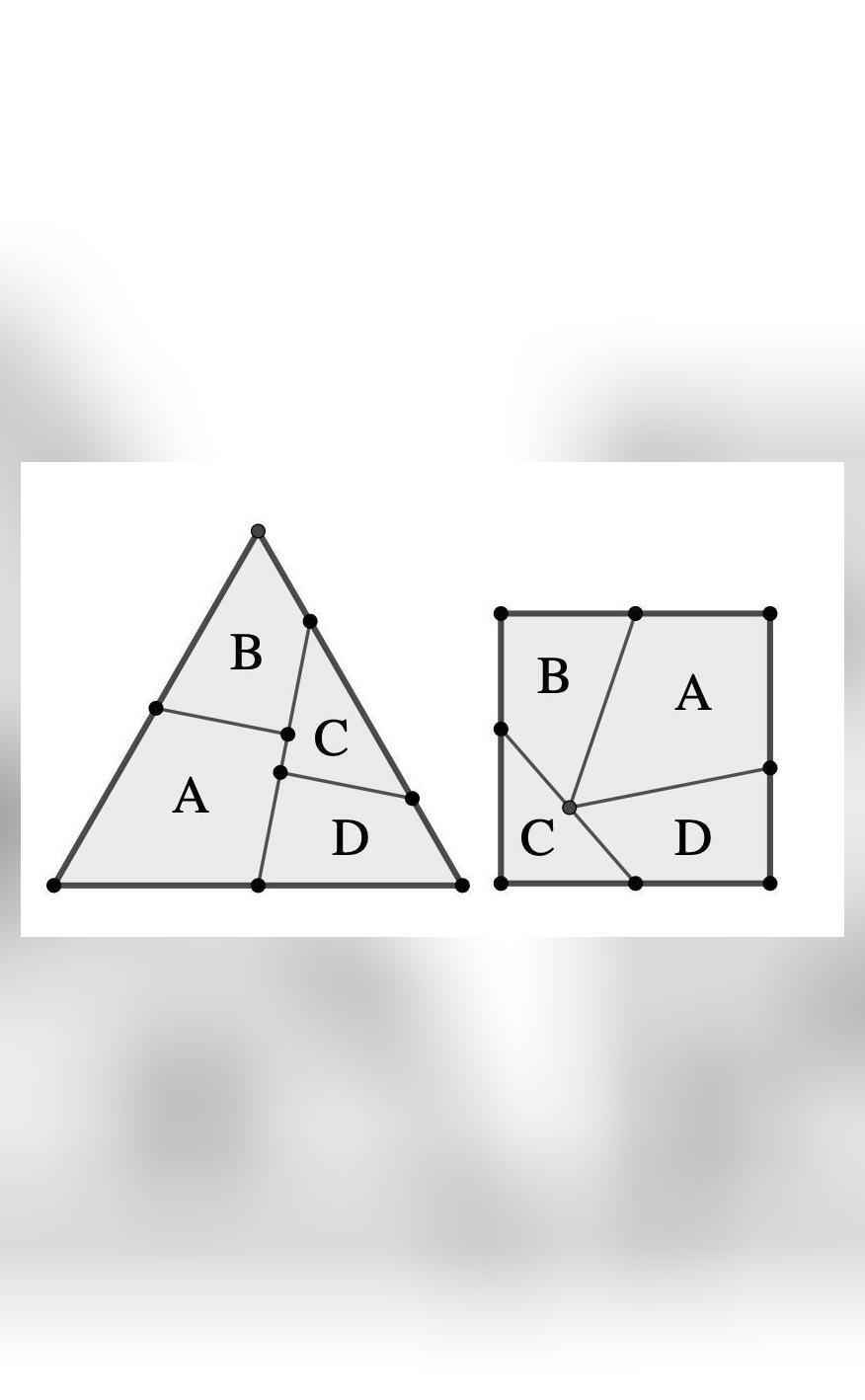
For over a century, mathematicians have been fascinated by the Dudeney’s dissection or haberdasher’s problem, a puzzle that has challenged the minds of many a brilliant mind. The problem, which involves dissecting an equilateral triangle into the smallest number of pieces to form a square, has finally been solved by a team of mathematicians from the United States and Japan. And the solution? A four-piece solution, just as proposed by English clerk Charles McElroy back in 1899.
The Dudeney’s dissection problem is a classic example of a “dissection problem,” where a shape is cut into a specific number of pieces and reassembled into another shape. In this case, the goal is to dissect an equilateral triangle into the smallest number of pieces possible, while maintaining the original shape and size, and then reassemble those pieces into a square.
Charles McElroy, an English clerk, was the first to propose a solution to this problem in 1899. His solution involved dissecting the triangle into four pieces, which could then be reassembled into a square. For over 120 years, this solution was considered the optimal solution, but mathematicians have long suspected that there might be a better way.
A team of mathematicians from the United States and Japan has now confirmed that McElroy’s solution is, in fact, the best possible solution. The team, led by mathematician Peter Brass from the University of California, San Diego, used advanced computer simulations and mathematical techniques to prove that a two-piece or three-piece solution is impossible.
The team’s findings were published in a recent issue of the journal Scientific American, and the news has sent shockwaves through the mathematical community. The confirmation of McElroy’s solution as the best possible solution is a major breakthrough, and it has significant implications for the field of geometry and mathematical problem-solving.
So, how did the team arrive at their conclusion? The answer lies in the development of advanced computer simulation techniques and mathematical algorithms. The team used a combination of computer simulations and mathematical proofs to demonstrate that a two-piece or three-piece solution is impossible.
The team’s approach involved using a technique called “polyominoes,” which are shapes composed of squares that can be connected in various ways. By analyzing the properties of these polyominoes, the team was able to show that any attempt to create a two-piece or three-piece solution would result in a shape that is not a square.
The team also used a technique called “tilings,” which involve covering a surface with shapes to create a pattern. By analyzing the tilings that would be required to create a two-piece or three-piece solution, the team was able to show that the resulting shape would not be a square.
The team’s findings have significant implications for the field of geometry and mathematical problem-solving. The confirmation of McElroy’s solution as the best possible solution provides a sense of closure and completion for mathematicians who have been working on this problem for over a century.
The Dudeney’s dissection problem is just one example of a broader class of problems known as “dissection problems.” These problems involve cutting a shape into a specific number of pieces and reassembling those pieces into another shape. Dissection problems are notoriously difficult to solve, and they often require the development of new mathematical techniques and algorithms.
The Dudeney’s dissection problem is also an example of the power of collaboration in mathematics. The solution to this problem was only possible because of the collaboration between mathematicians from the United States and Japan. This collaboration highlights the importance of international collaboration in mathematics, and it provides a model for how mathematicians from different countries can work together to solve complex problems.
In conclusion, the solution to the Dudeney’s dissection problem is a major breakthrough in the field of mathematics. The confirmation of McElroy’s solution as the best possible solution provides a sense of closure and completion for mathematicians who have been working on this problem for over a century. The solution also highlights the importance of collaboration in mathematics, and it provides a model for how mathematicians from different countries can work together to solve complex problems.
Source: